La línea recta es una figura representada en el plano formada por una sucesión de puntos en una sola dirección. También se entiende como:
- Una sucesión de puntos que son colineales.
- La distancia mas corta que hay entre dos puntos.

Nota: Las rectas se nombran con letras minúsculas y los puntos con letras mayúsculas.
La semirrecta. Si colocamos un punto sobre una recta quedará dividida en dos semirrectas, esto quiere decir que una semirrecta es una recta que tiene principio y no tiene fin (se prolonga infinitamente).

La figura anterior representa una recta que tiene un origen en el punto A y se prolonga infinitamente, por lo tanto es una semirrecta m.
Un segmento es una recta que va de un punto a otro, la distancia mas corta que hay entre dos puntos, tiene un principio y un fin, por lo tanto tiene una longitud definida.
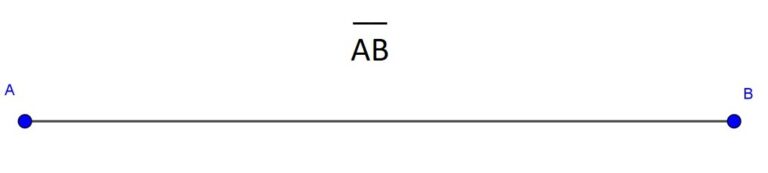
La figura anterior representa el segmento AB, una recta que va del punto A al punto B o viceversa. Se denota con una linea recta sobre las letras de los puntos que la delimitan. Veamos los ejemplos:
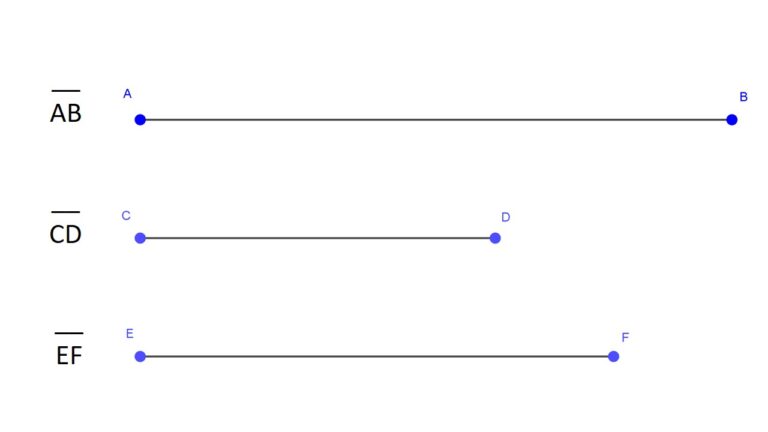
En la figura anterior podemos observar los ejemplos de los segmentos AB, CD y EF.
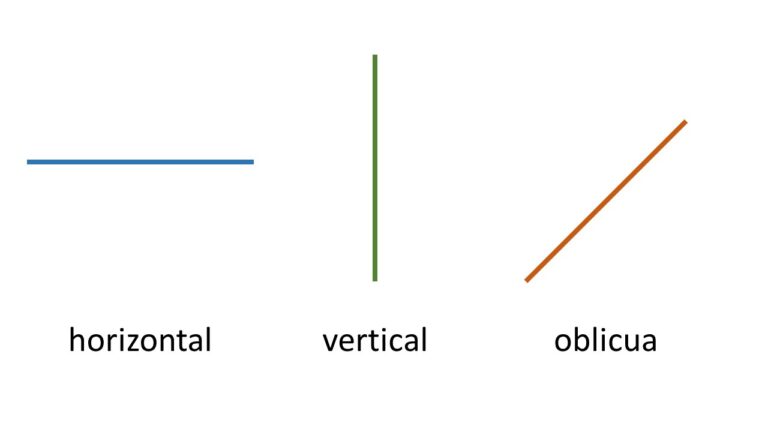
Las rectas se pueden clasificar de acuerdo a la posición que tienen en el espacio:
- Horizontales.
- verticales.
- Oblicuas.
Una recta horizontal es aquella que tiene pendiente cero, es decir, que no forma ningún ángulo. Una recta horizontal se representa en el plano cartesiano como una recta que es paralela al eje x (eje de las abscisas).
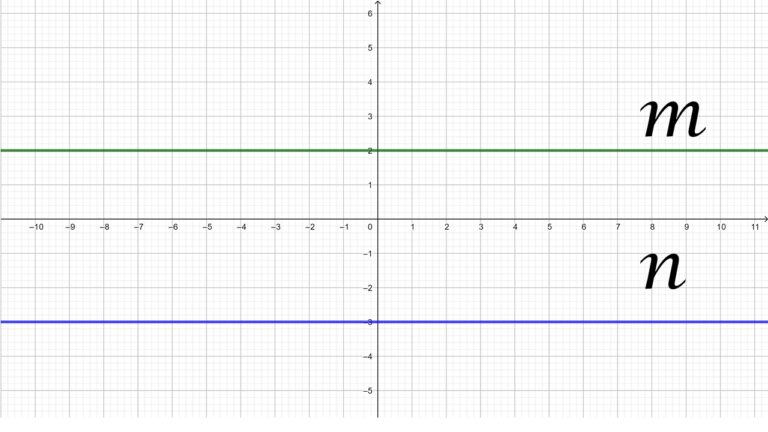
En la imagen anterior se observan las rectas m y n, estas rectas son horizontales ya que tienen pendiente cero y ambas son paralelas al eje x.
Las rectas verticales son aquellas que tienen pendiente de 90°, son paralelas al eje «y» del plano cartesiano (eje de las ordenadas).
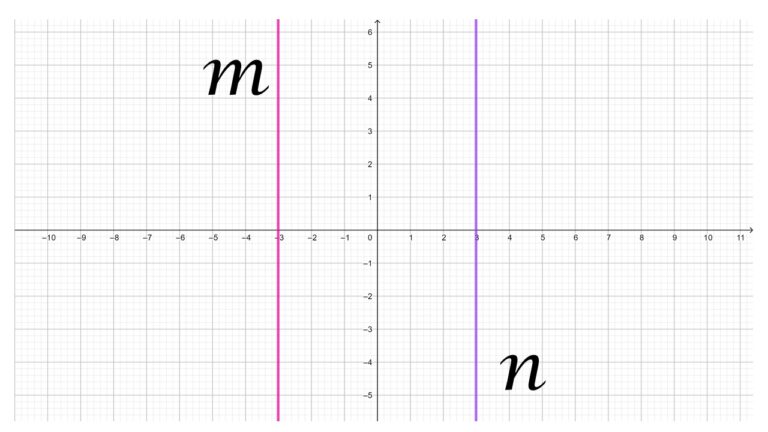
En la imagen anterior se observan las rectas m y n, ambas rectas son verticales porque tienen pendiente de 90° con respecto al eje x, ambas rectas son paralelas al eje y.
Las rectas oblicuas (también llamadas diagonales o inclinadas), son aquellas que tienen una pendiente mayor que cero y diferente que 90°.
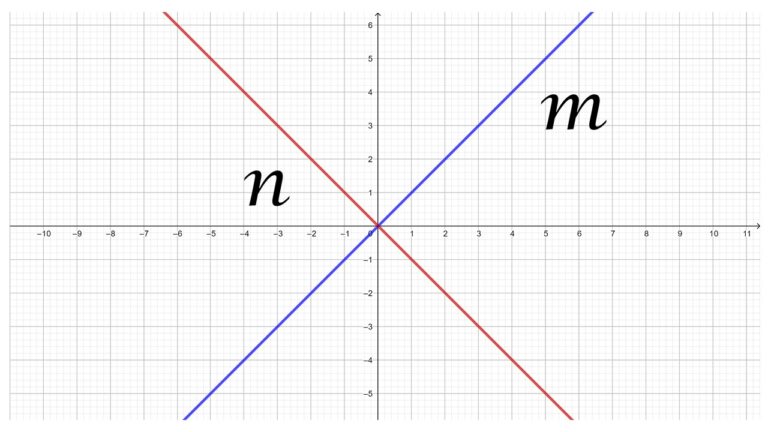
En la imagen anterior se observan las rectas m y n, estas rectas son oblicuas porque tienen pendiente mayor que 0° y diferente que 90°, no son paralelas al eje x ni al eje y.
Las rectas oblicuas tienen pendiente positiva o pendiente negativa, observa los siguientes ejemplos:
- Las rectas oblicuas con pendiente positiva son aquellas que tienen un ángulo de inclinación menor a 90° con respecto al eje x.
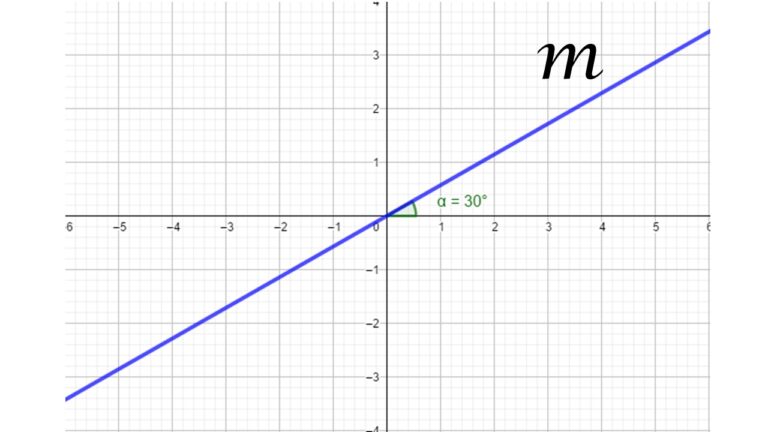
En la imagen anterior se observa una recta oblicua con pendiente positiva ya que su ángulo de inclinación con respecto al eje x es menor que 90°.
- Las rectas oblicuas con pendiente negativa son aquellas que tienen un ángulo de inclinación mayor a 90° y menor a 180° con respecto al eje x.
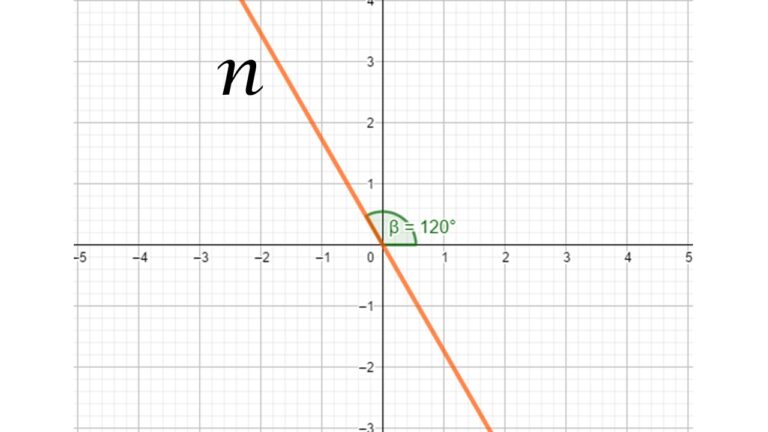
En la imagen anterior se observa una recta oblicua con pendiente negativa ya que su ángulo de inclinación con respecto al eje x es mayor que 90° y menor que 180°.
Ademas de las clasificaciones anteriores, las rectas también se pueden clasificar de acuerdo con la relación que mantienen entre ellas, las cuales son:
- Rectas paralelas.
- Rectas perpendiculares.
- Rectas secantes.
Las rectas paralelas son aquellas que están situadas en un mismo plano y nunca se cortan por más que se prolonguen.
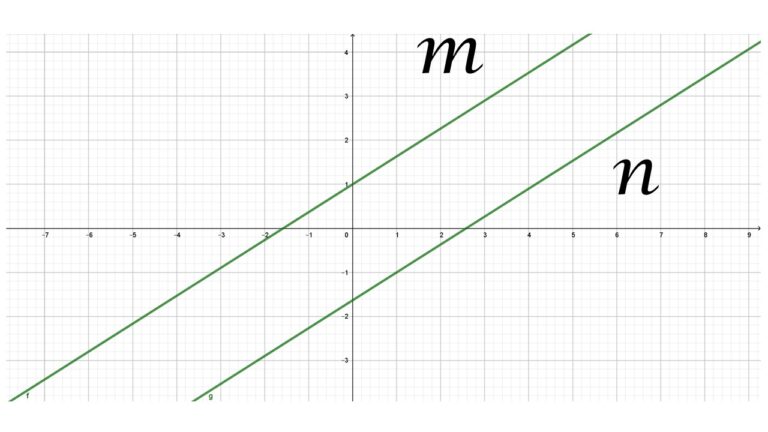
En la imagen anterior las rectas m y n son paralelas.
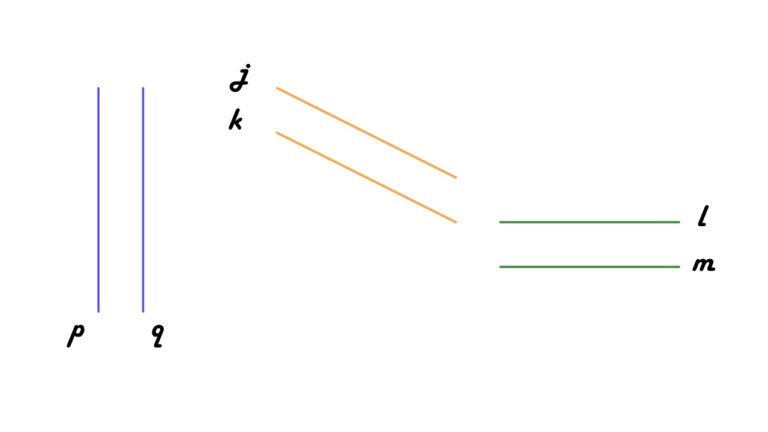
En la imagen anterior se muestran tres pares de rectas paralelas:
- p es paralela con q.
- j es paralela con k.
- l es paralela con m.
Las rectas perpendiculares son aquellas que están situadas en un mismo plano y se cortan formando cuatro ángulos de 90°.
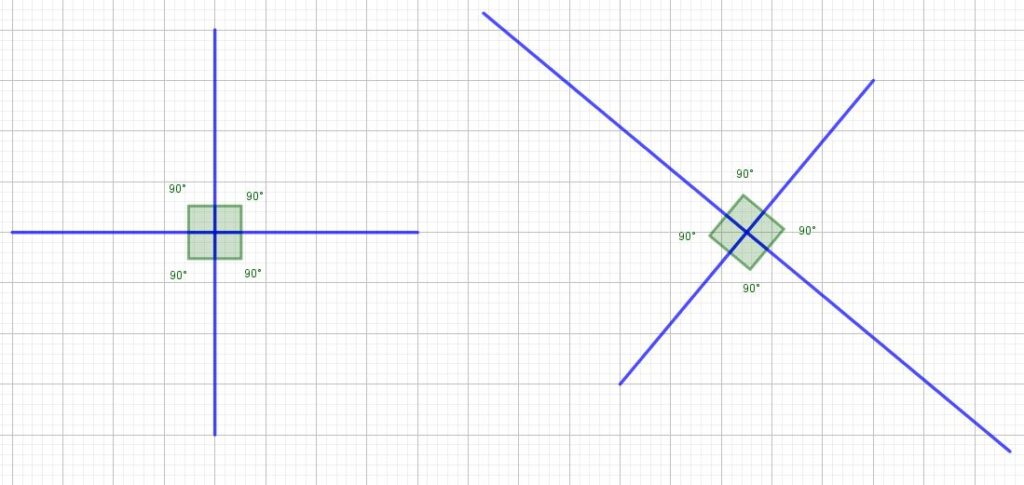
En la imagen anterior se observan dos pares de rectas perpendiculares, el primero de ellos formado por una recta horizontal y otra vertical, el segundo par de perpendiculares está formado por dos rectas oblicuas.
Las rectas secantes son aquellas que se cortan en un punto formando un par de ángulos agudos y un par de ángulos obtusos.
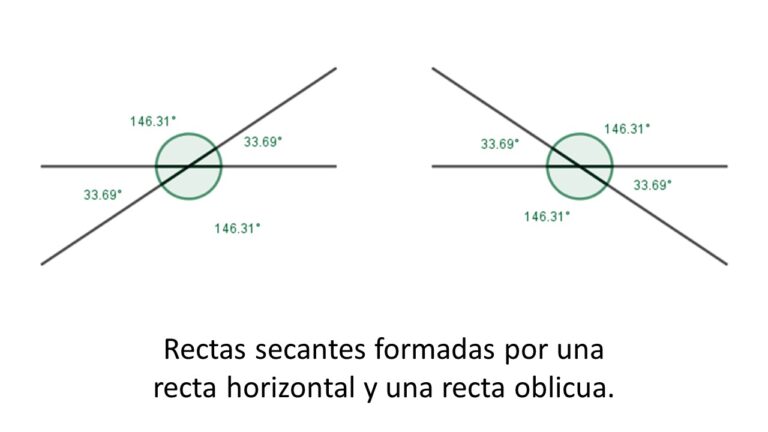
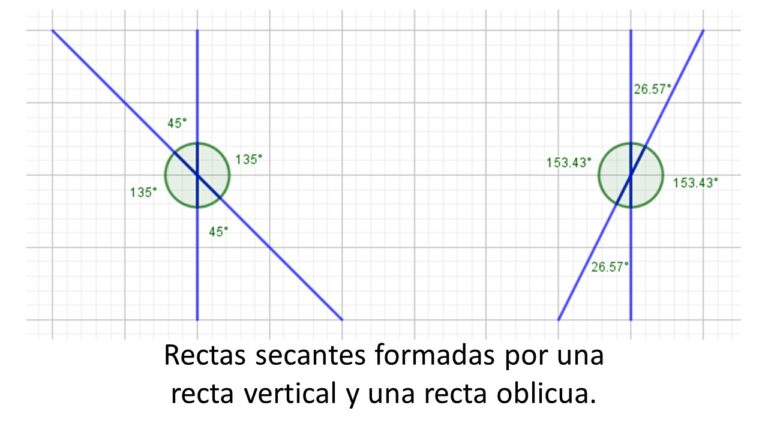
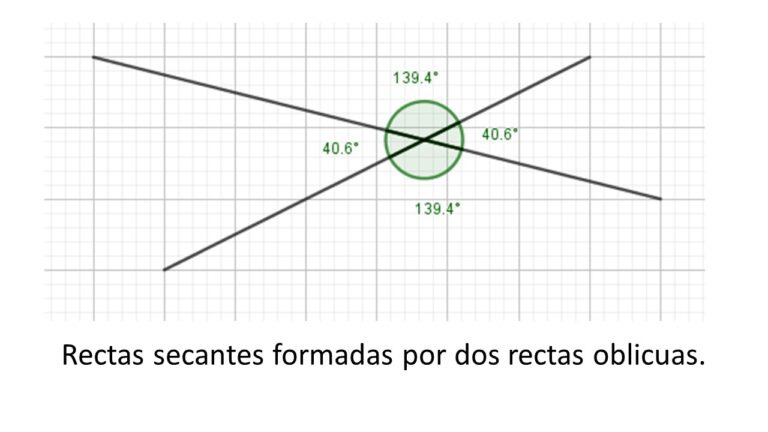
En el carrusel de imágenes anterior se observan distintas formas de representar dos rectas secantes.
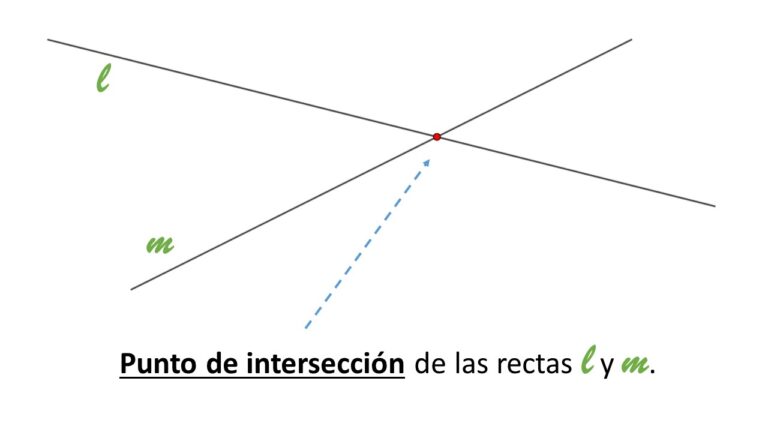
El punto donde se cortan dos rectas se conoce como punto de intersección.