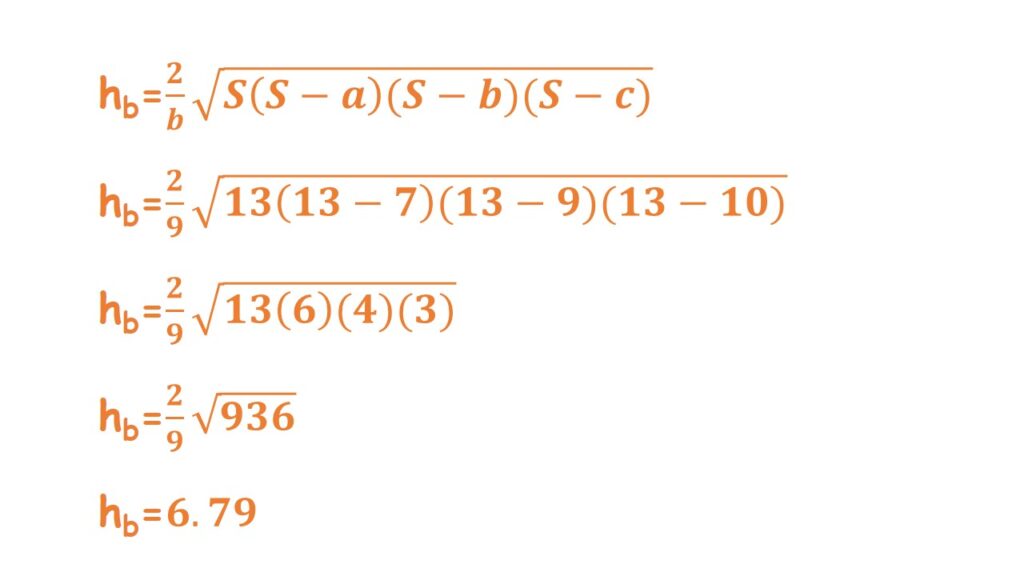La altura de un triángulo se puede definir de las siguientes formas:
- Es la distancia vertical que hay de la base del triángulo hacia el vértice opuesto a la base.
- Es la longitud del segmento perpendicular de uno de sus lados hacia su vértice opuesto.
Para medir la altura de un triángulo es necesario colocar uno de sus lados de forma horizontal, a este lado se le denomina base.
- TRIÁNGULO EQUILÁTERO E ISÓSCELES. Su altura (h) es la distancia que hay del punto medio de la base (P) al vértice opuesto.
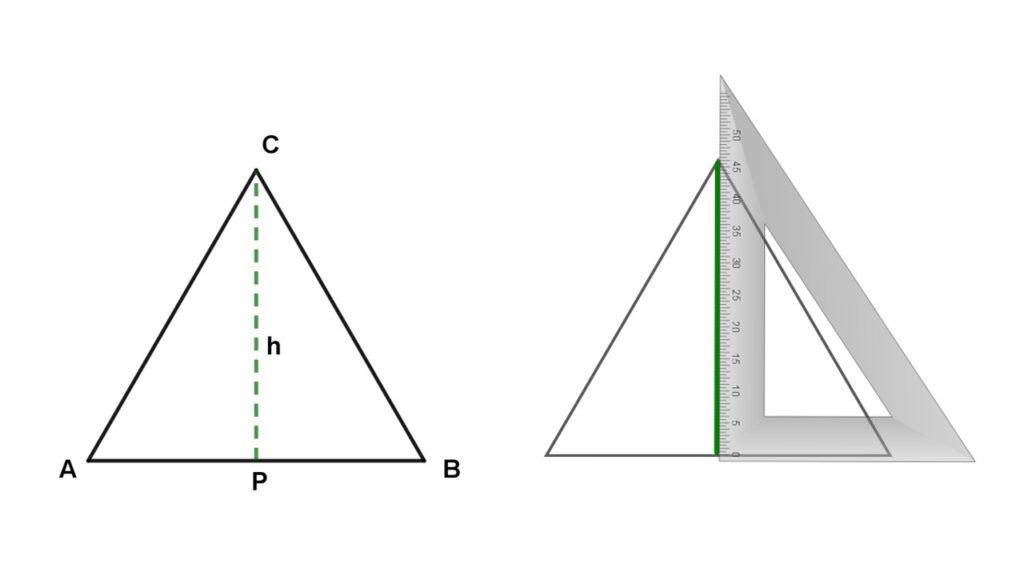
- TRIÁNGULO ESCALENO , ACUTÁNGULO Y OBTUSÁNGULO. Su altura (h) es la distancia vertical que hay del vértice opuesto a su base o prolongación de ésta.
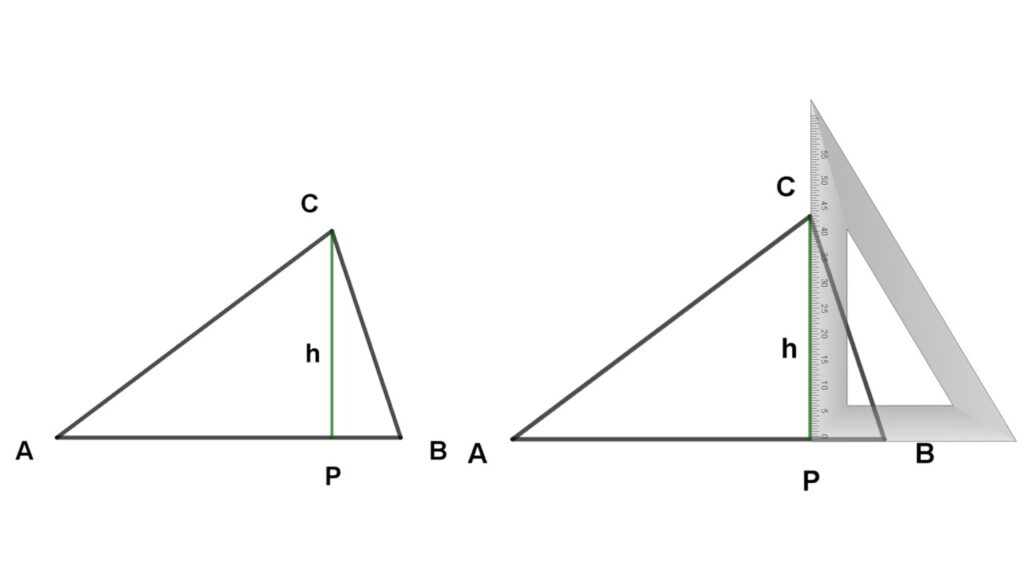
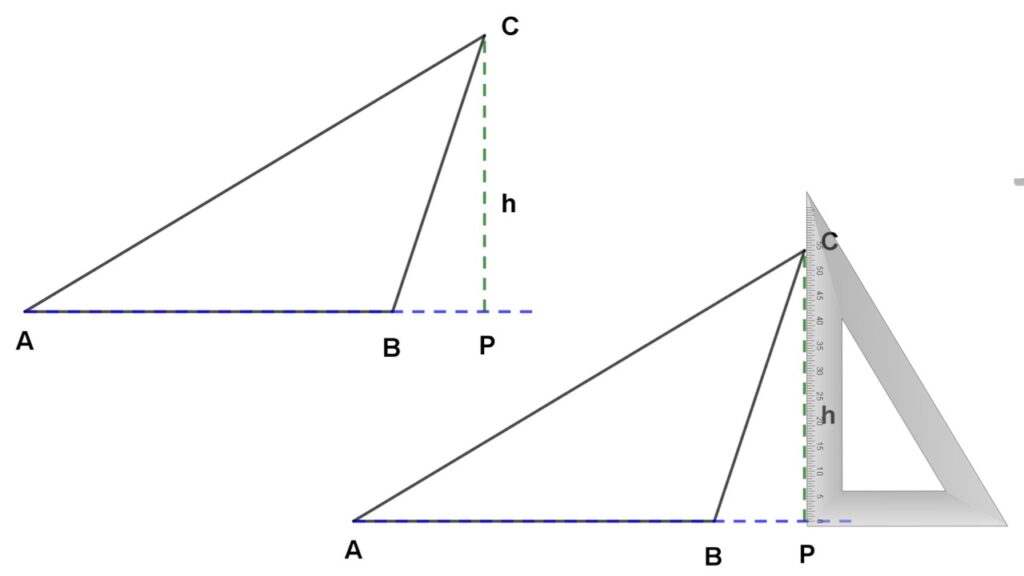
- TRIÁNGULO RECTÁNGULO. La altura de un triángulo rectángulo cuya base es uno de sus catetos se mide de uno de los extremos de la base hacia su vértice opuesto.
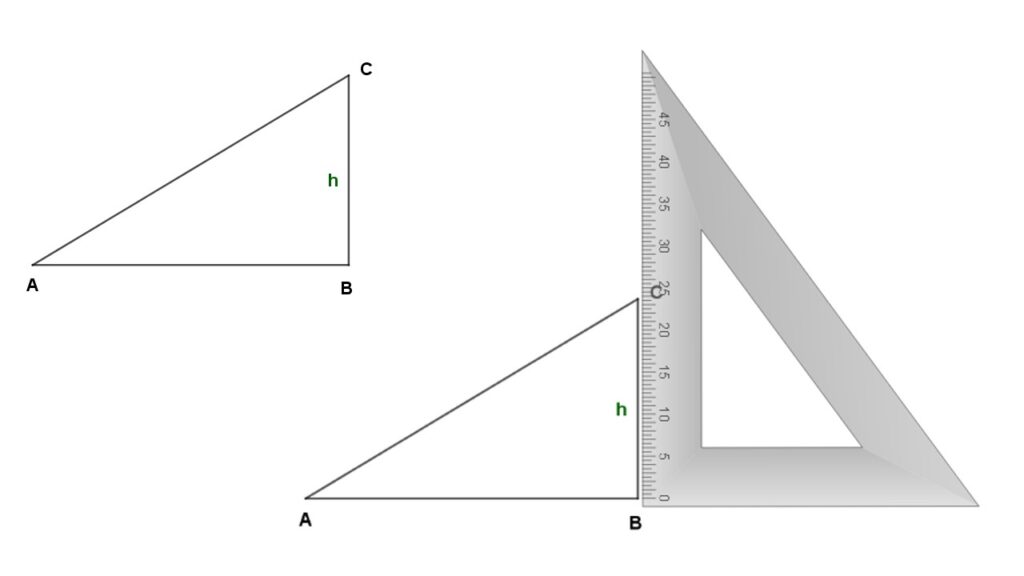
Calcular la altura del triangulo mediante el Teorema de Pitágoras.
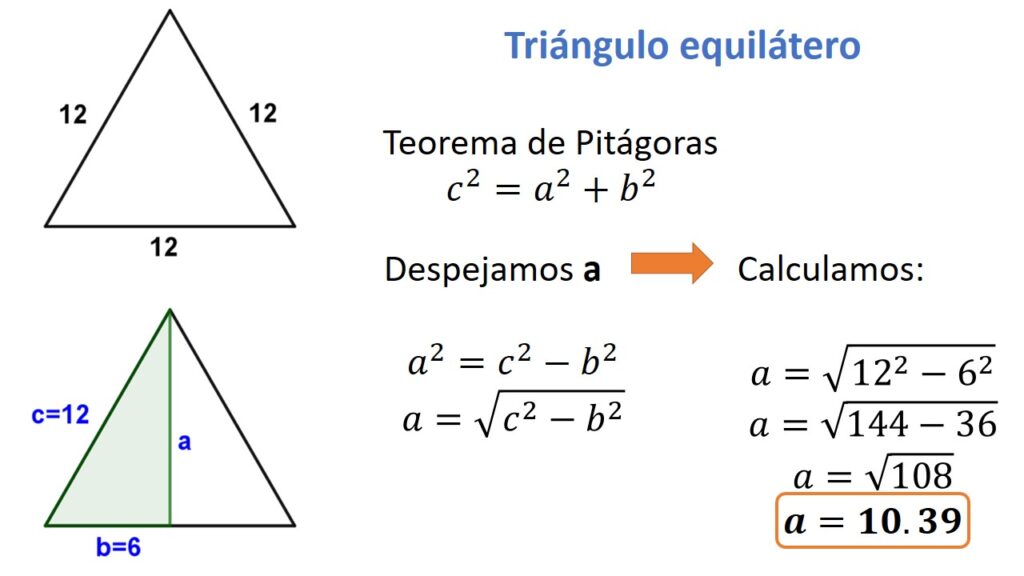
EN TRIÁNGULOS EQUILÁTEROS E ISÓSCELES.
- Se ubica el punto medio de la base (P) y se traza un segmento de P al vértice opuesto a la base.
- Se renombran a y b como los catetos de uno de los dos triángulos rectángulos que se formaron.
- Se calcula la mitad de la base para obtener la medida de uno de los catetos.
- La hipotenusa (c) es el lado opuesto al ángulo de 90° que se forma del punto medio de la base a su vértice opuesto
- Se aplica el Teorema de Pitágoras despejando el cateto a que representa a la altura del triángulo.
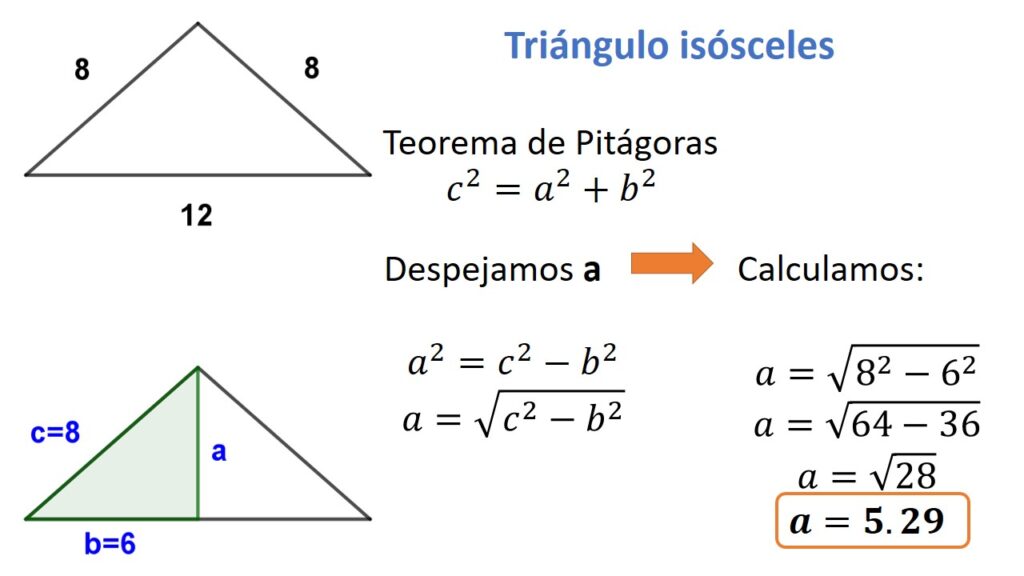
EN UN TRIÁNGULO RECTÁNGULO.
Cuando un triángulo rectángulo tiene como base uno de sus catetos y se desconoce la medida de su altura, se aplica el Teorema de Pitágoras.
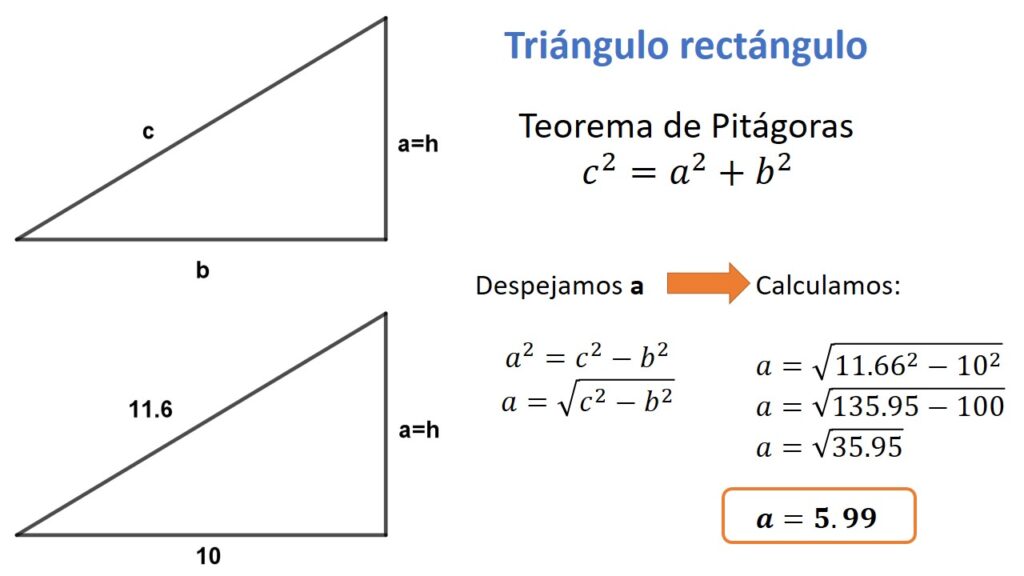
Calcular las alturas de un triángulo de acuerdo con la medida de sus lados.
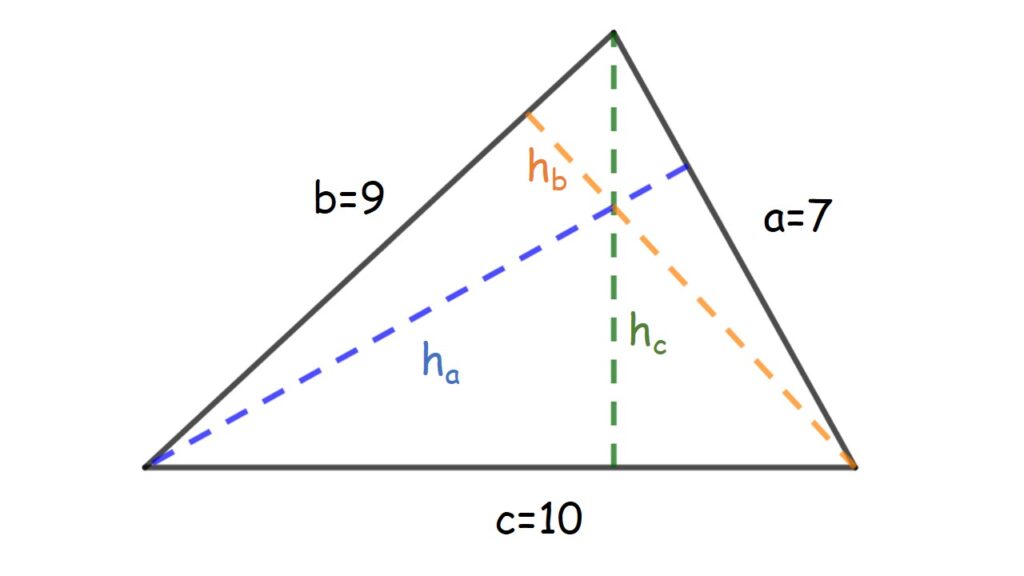
Cuando se conoce la medida de los lados de un tríángulo se pueden aplicar las siguientes formulas para calcular cualquiera de sus tres alturas.
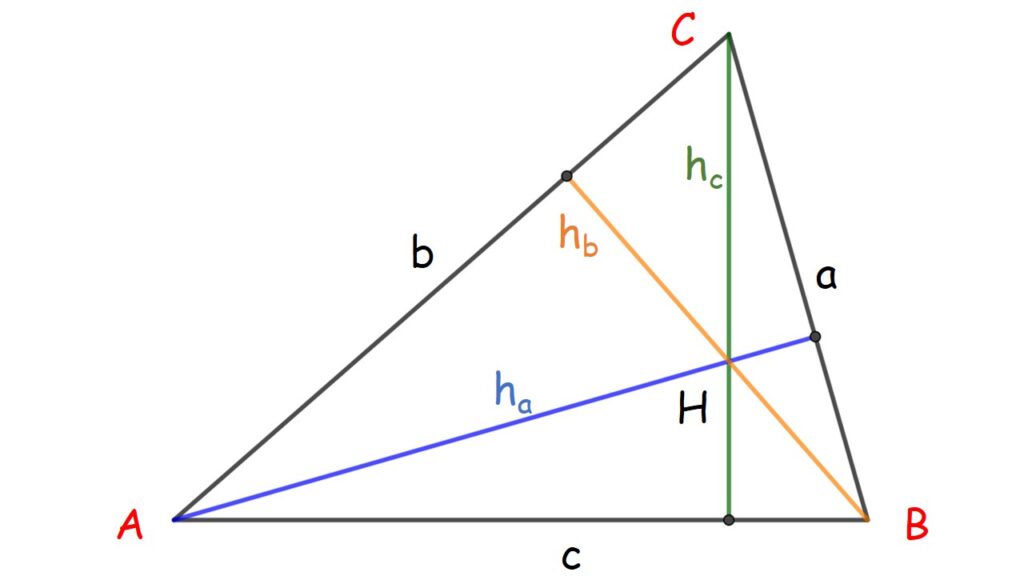
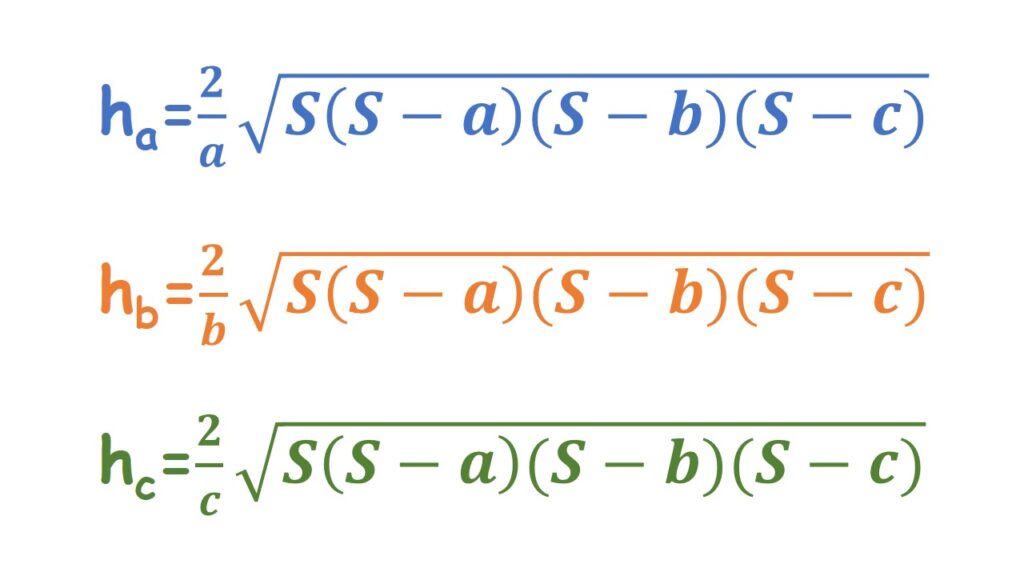
Donde:
- A, B y C son los vértices del triángulo.
- a, b y c son los lados del triángulo.
- ha= altura a
- hb= altura b
- hc= altura c
- S= semiperímetro
- H= ortocentro
El semiperímetro de un triángulo es la mitad de su perímetro es decir:
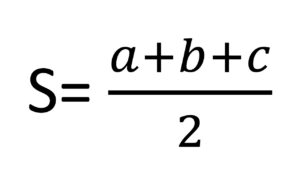
Veamos el siguiente ejemplo: